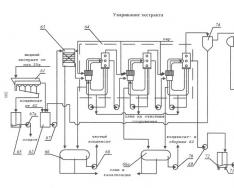
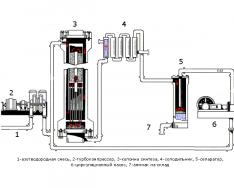
Ez a cikk teljes mértékben a KD-Trees-nek szentelt: leírom a KD-Trees felépítésének finomságait, a KD-Tree "közeli" keresési funkcióinak megvalósításának finomságait, valamint a megoldás során felmerülő lehetséges "csapdákat". az algoritmus egyes részfeladatai. Annak érdekében, hogy ne keverjük össze az olvasót a terminológiával (sík, hipersík stb.), sőt a kényelem kedvéért feltételezzük, hogy a fő cselekmény háromdimenziós térben zajlik. Ahol azonban szükséges, megjegyzem, hogy más dimenziójú térben dolgozunk. Véleményem szerint a cikk hasznos lesz mind a programozóknak, mind mindazoknak, akik érdeklődnek az algoritmusok tanulmányozása iránt: valaki valami újat talál magának, valaki pedig egyszerűen megismétli az anyagot, és esetleg kiegészíti a cikket a megjegyzésekben. Mindenesetre kérek mindenkit kat alá.

Bevezetés

KD fa(K-dimenziós fa), egy speciális "geometrikus" adatstruktúra, amely lehetővé teszi, hogy egy K-dimenziós teret "kisebb részekre" bontsa fel úgy, hogy ezt a teret hipersíkokkal ( K > 3), repülőgépek ( K = 3), egyenes vonalak ( K = 2) nos, és egydimenziós ponttér esetén (ilyen fában keresve valami hasonlót kapunk bináris keresés).
Logikus, hogy egy ilyen partíciót általában a keresési tartomány szűkítésére használnak a K-dimenziós térben. Például közeli objektum (csúcs, gömb, háromszög stb.) keresése egy ponthoz, pontok kivetítése 3D-s hálóra, sugárkövetés (aktívan használatos a Ray Tracingben) stb. Ebben az esetben az űrobjektumokat speciális paralelepipedonokba helyezik - határoló dobozok(határolókeretnek nevezzük az olyan dobozt, amely az objektumok eredeti halmazát vagy magát az objektumot írja le, ha csak neki építünk határolókeretet. Pontoknál a nulla felületű és nulla térfogatú határolódobozt vesszük határolónak. doboz), melynek oldalai párhuzamos koordinátatengelyek.

Csomópont felosztási folyamat

Tehát a KD-Tree használata előtt meg kell építeni. Az összes objektumot egyetlen nagy határolódobozba helyezzük, amely leírja az eredeti halmaz objektumait (mindegyik objektumot a saját határoló doboza korlátoz), amelyet ezután az egyik oldalával párhuzamos sík kettéválaszt (oszt). Két új csomópont hozzáadódik a fához. Ugyanígy a kapott paralelepipedonok mindegyikét két részre osztjuk, és így tovább. A folyamatot vagy egy speciális kritérium zárja le (lásd SAH), vagy ha a fa egy bizonyos mélységét eléri, vagy ha egy fa csomópontján belül bizonyos számú elemet elér. Egyes elemek egyszerre léphetnek be a bal és a jobb oldali csomópontokba (például ha a háromszögeket faelemeknek tekintjük).

Ezt a folyamatot egy háromszöghalmaz példáján fogom bemutatni 2D-ben:

A 1. ábra a háromszögek kezdeti halmaza látható. Minden háromszög a saját határolókeretébe kerül, és a teljes háromszöghalmaz egy nagy gyökérhatároló dobozba van beírva.

A 2. ábra a gyökércsomópontot két csomópontra osztjuk (OX szerint): az 1, 2, 5 háromszögek a bal, a 3, 4, 5 pedig a jobb csomópontba esnek.

A 3. ábra, a kapott csomópontokat ismét két részre osztjuk, és mindegyikbe belép az 5-ös háromszög. Amikor a folyamat véget ér, 4 levélcsomópontot kapunk.

Nagyon fontos a fa csomópontjának felosztására szolgáló sík kiválasztása. Ennek nagyon sok módja van, csak néhányat adok a gyakorlatban legelterjedtebb módszerek közül (feltételezzük, hogy a kezdeti objektumok egy nagy határolódobozban vannak elhelyezve, és a felosztás az egyik koordinátatengellyel párhuzamosan történik) :

⦁ 1. módszer: Válassza ki a határolókeret legnagyobb oldalát. Ezután a vágási sík áthalad a kiválasztott oldal közepén.

⦁ 2. módszer: Szelet medián szerint: az összes primitív rendezése valamelyik koordináta szerint, és a medián az az elem (vagy az elem közepe), amely a rendezett lista középső pozíciójában van. A vágási sík átmegy a mediánon, így a bal és jobb oldali elemek száma megközelítőleg egyenlő lesz.

⦁ 3. módszer: Változó oldalak használata hasításnál: 0 mélységben a párhuzamos oldal OX közepén átütjük, a következő mélységi szint az OY párhuzamos oldal közepén, majd OZ mentén stb. Ha „minden tengelyen végigmentünk”, akkor újra kezdjük a folyamatot. A kilépési feltételeket fentebb ismertettük.

⦁ 4. módszer: A legokosabb lehetőség a használata SAH (felszíni heurisztika) határoló doboz osztott kiértékelési funkciója. (Erről az alábbiakban részletesen lesz szó). Az SAH egy univerzális kritériumot is biztosít a csomópontosztás leállítására.

1. és 3. módszer jók, ha a fa építésének sebességéről van szó (hiszen egy oldal közepének megtalálása és sík rajzolása rajta, az eredeti halmaz elemeinek kiszűrése "balra" és "jobbra" triviális) . Ugyanakkor gyakran lazán ábrázolják a tér felosztását, ami negatívan befolyásolhatja a KD-Fa alapműveleteit (különösen, ha egy sugarat nyomon követünk egy fában).

2. módszer lehetővé teszi jó eredmények elérését, de jelentős időt igényel, amelyet a csomópont elemeinek rendezésére fordítanak. Az 1. és 3. módszerekhez hasonlóan meglehetősen egyszerű a megvalósítása.

A legérdekesebb az „intelligens” SAH-heurisztikát használó módszer (4. módszer).

Egy fa csomópont határolókeretét N (a tengelyekkel párhuzamos) sík osztja N + 1 részre (a részek általában egyenlőek) mindkét oldalon (valójában az oldalak síkjainak száma tetszőleges lehet, de az egyszerűség kedvéért és a hatékonyságot állandónak veszik) . Továbbá a sík és a határolókeret lehetséges metszéspontjainál a speciális függvény értékét számítjuk ki: SAH. Az osztást az SAH függvény legkisebb értékű síkja csinálja (az alábbi ábrán azt feltételeztem, hogy SAH-ban elérjük a minimumot, ezért az osztást ez a konkrét sík fogja megtenni (bár itt a 2D tér kb. egyenes)):

Az SAH függvény értékét az aktuális síkra a következőképpen számítjuk ki:

A KD Tree implementációmban minden oldalt 33 egyenlő részre osztok 32 sík segítségével. Így a teszteredmények szerint sikerült megtalálnom az "arany középutat" - a fa fő funkcióinak sebességét / a fa építésének sebességét.

SAH heurisztikaként a fenti ábrán látható függvényt használom.

Megjegyzendő, hogy ennek a funkciónak csak a minimuma szükséges az összes vágási síkon a döntéshez. Ezért az egyenlőtlenségek legegyszerűbb matematikai tulajdonságait felhasználva, valamint a 2-vel való szorzást elvetve a csomópont felületének kiszámításakor (3D-ben) ( SAR, SAL, SA), ez a képlet jelentősen leegyszerűsíthető. Teljes mértékben a számításokat csak egyszer hajtják végre csomópontonként: az osztási függvényből való kilépési kritérium kiértékelésekor. Egy ilyen egyszerű optimalizálás jelentősen megnöveli a fa építésének sebességét ( x2.5).

Egy függvény SAH értékének hatékony kiszámításához gyorsan meg kell tudni határozni, hány csomóponti elem van egy adott síktól jobbra, és hány balra. Nem lesz kielégítő az eredmény, ha a durva, ún nyers erő másodfokú aszimptotikával való megközelítés. Használatakor azonban "kosár" (bedobva) módszer szerint a helyzet jelentősen javul. Ennek a módszernek a leírása az alábbiakban található:

Tegyük fel, hogy a határolókeret oldalát N egyenlő részre osztjuk (síkok száma-(N-1)), a határolókeret egy koordinátapárban tárolódik (pointMin, pointMax-lásd. rizs. egy), akkor egy menetben a csomópont összes elemén pontosan meg tudjuk határozni minden síkra, hogy hány elem van attól jobbra és hány balra. Hozzunk létre két tömböt egyenként N elemmel, és inicializáljuk őket nullákkal. Legyen névvel ellátott tömbök magasés aLow. Sorban végigfutjuk a csomópont összes elemét. Az aktuális elemnél ellenőrizzük, hogy a határolókeret pointMin és pointMax melyik részébe esik. Ennek megfelelően a halmaz elemenként két indexet kapunk. Legyen névmutatók iHigh(pontMax esetén) és iLow(pontMin-hez). Ezt követően tegye a következőket: aHigh += 1, aLow +=1.

Miután áthaladtunk az összes elemen, megkapjuk a kitöltött aHigh és aLow tömböket. Az aHigh tömbhöz a részleges utótag (utótag) összegét, az aLow esetében pedig a részleges előtag (előtag) összegét számítjuk (lásd az ábrát). Kiderül, hogy a jobb oldalon lévő elemek száma ( és csak jobbra!) az i indexű síkból egyenlő lesz aLow-val, a balra eső elemek száma ( és csak a bal oldalon!): aHigh[i], a bal és a jobb oldali csomópontban is szereplő elemek száma: AllElements-aLow-aHigh[i].

A feladat megoldása megtörtént, ennek az egyszerű folyamatnak az illusztrációja az alábbiakban látható:

Szeretném megjegyezni, hogy a "verés" síktól balra és jobbra előre ismert számú elem elhelyezése lehetővé teszi, hogy előre lefoglaljuk számukra a szükséges memóriamennyiséget (mivel a továbbiakban a minimális SAH megszerzése után kell újra végigmenni az összes elemen, és mindegyiket a kívánt tömbbe helyezni, (és a banális push_back használata (ha nem hívták meg a tartalékot) állandó memóriafoglaláshoz vezet - ez nagyon költséges művelet), ami pozitívan befolyásolja a faépítési algoritmus (x3.3).

Most szeretném részletesebben leírni az SAH kiszámítására szolgáló képletben használt állandók célját, és beszélni a csomópont felosztásának leállításának kritériumáról.

Folyamatosan körözve az állandókon cIés cT, az algoritmus futási idejének feláldozásával sűrűbb fastruktúra érhető el (vagy fordítva). Számos cikkben, amelyek elsősorban egy KD-Tree for Ray Tracing render létrehozásával foglalkoznak, a szerzők az értékeket használják cI = 1., cT =: minél nagyobb a cT értéke, annál gyorsabban épül fel a fa, és annál rosszabb lesz a sugárkövetés eredménye egy ilyen fában.

Saját megvalósításomban egy fát használok a "szomszéd" keresésére, és megfelelő figyelmet fordítva a tesztelés eredményeire és a szükséges együtthatók keresésére, láthatja, hogy a cT magas értékei olyan csomópontokat adnak nekünk, amelyek teljesen nem sűrűn tele elemekkel. Ennek elkerülése érdekében úgy döntöttem, hogy a cT értéket 1-re állítom, és a cI értéket különböző nagy adategységeken tesztelem. Ennek eredményeként meglehetősen sűrű faszerkezetet lehetett kapni, amely jelentősen megnövelte az építési időt. Ez az akció pozitív hatással volt a "szomszéd" keresésének eredményeire - a keresés sebessége megnőtt.

A csomópont felosztásának leállításának kritériuma meglehetősen egyszerű:

Más szavakkal: Ha a gyermekcsomópontok nyomon követésének költsége nagyobb, mint a szülőcsomópont követésének költsége, akkor a felosztást le kell állítani.

Most, hogy megtanultuk, hogyan kell felosztani egy KD-Tree csomópontot, elmesélem azokat a kezdeti eseteket, amikor a csomópont elemeinek száma elég nagynak bizonyul, és az elemek számával való leállítási kritérium az algoritmushoz vezet. végtelenség. Valójában minden figyelem a képre irányul (a háromszögek példájával 2D-ben):

Én ezeket a helyzeteket hívom "ventilátor"(van közös érintkezési pontjuk, egybeeső tárgyak, én is erre a kategóriára hivatkozom). Látható, hogy hiába rajzoljuk meg a vágási síkot, a középpont valahogy beleesik az egyik csomópontba, és vele együtt azok a háromszögek, amelyekre közös.

Faépítési folyamat

Megtanultuk, hogyan kell felosztani egy fa csomópontot, most már csak a megszerzett ismereteket kell alkalmazni a teljes fa felépítésére. Az alábbiakban bemutatom a KD-Tree felépítésének megvalósítását.

A fa a gyökérből épül fel. A fa minden csomópontjában tárolok mutatókat a bal és a jobb részfára, ha a csomópontnak nincs ilyen, akkor a rendszer figyelembe veszi lap(lap pl.). Minden csomópont tárol egy határoló dobozt, amely leírja az adott csomópontban lévő objektumokat. lapon( és csak lapokban!) csomópontokat, tárolom azon objektumok indexeit, amelyek ebben a csomópontban szerepelnek. Az építési folyamat során azonban a csomópontok memóriája részletekben van lefoglalva (vagyis K csomóponthoz egyszerre: egyrészt hatékonyabb a memóriakezelővel való munka, másrészt az egymást követő elemek ideálisak a gyorsítótárazáshoz). Ez a megközelítés megtiltja a fa csomópontjainak vektorban való tárolását, mivel új elemek hozzáadása egy vektorhoz az összes meglévő elem memória átcsoportosításához vezethet egy másik helyre.

Ennek megfelelően a részfákra mutató mutatók minden jelentésüket elvesztik. Lista típusú tárolót (std::list) használok, amelynek minden eleme egy vektor (std::vector), előre meghatározott mérettel (konstans). A fát többszálasan építem fel (Open MP-t használok), vagyis minden részfát külön szálban építek (x4 sebességre). Az indexek levél csomópontba való másolásához a mozgatási szemantika (C++11) (+10% sebesség) az ideális.

A „legközelebbi” pont megkeresése a KD-fában

Tehát a fa elkészült, térjünk át a keresési művelet végrehajtásának leírására a KD-Tree-ben.

Tegyük fel, hogy háromszögek halmazában keresünk: adott ponton meg kell találnunk a hozzá legközelebb eső háromszöget.

A probléma megoldása bruteforce használatával veszteséges: N pontból és M háromszögből álló halmaz esetén az aszimptotika O(N * M) lesz. Ezen kívül szeretném, ha az algoritmus "őszintén" kiszámolná egy pont és a háromszög távolságát, és gyorsan megtenné.

Használjuk a KD-fát, és tegyük a következőket:

⦁ 1. lépés. Keressük meg az adott ponthoz legközelebbi levélcsomópontot (minden csomópontban, mint tudod, tároljuk a határolókeretet, és nyugodtan kiszámolhatjuk a csomópont határolókeretének középpontjától való távolságot ((pontMax + pontMin) * 0,5) és jelölje a legközelebbi csomópontot.

⦁ 2. lépés. A talált csomópont (nearestNode) összes elemén keresztül iterálva. Jelöljük a kapott távolságot minDist-ként.

⦁ 3. lépés. Építsünk egy gömböt, amelynek középpontja a kiindulási pontban van, és amelynek sugara minDist. Ellenőrizzük, hogy ez a gömb a legközelebbi csomóponton belül van-e teljesen (vagyis a határoló doboz-csomópont oldalainak metszéspontja nélkül). Ha hazudik, akkor a legközelebbi elem megtalálható, ha nem, akkor folytassa a 4. lépéssel.

⦁ 4. lépés. Kezdjük a fa gyökerétől, keressük a sugárban a legközelebbi elemet: a fán lefelé haladva ellenőrizzük, hogy a jobb vagy a bal csomópontok vannak-e (ráadásul a csomópont teljesen a gömbön belül feküdhet, vagy a gömb a csomóponton belül). ..) metszik az adott gömböt. Ha bármelyik csomópontot bejártuk, akkor hasonló ellenőrzést végzünk ugyanazon csomópont belső csomópontjaira. Ha egy levélcsomóponthoz jutottunk, akkor iteratív keresést hajtunk végre ebben a csomópontban a legközelebbi csomópontra, és az eredményt összehasonlítjuk a gömb sugarának hosszával. Ha a gömb sugara nagyobb, mint a talált távolság, frissítse a gömb sugarának hosszát a számított minimális értékkel. A fa mentén további ereszkedések a gömb sugarának frissített hosszával történnek (ha rekurzív algoritmust használunk, akkor a sugár egyszerűen átadódik a függvénynek hivatkozással, majd szükség esetén frissítjük).

Az alábbi ábra segít megérteni a fent leírt algoritmus lényegét:

rajz szerint: tegyük fel, hogy egy adott ponthoz (pirossal kiemelve) megtaláltuk a legközelebbi levélcsomópontot (az ábrán kék), akkor a csomópontban lévő legközelebbi csomópont keresése után azt kapjuk, hogy ez egy 1 indexű háromszög, azonban mint látod, ez nem így van. Az R sugarú kör egy szomszédos csomópontot metsz, ezért ezen a csomóponton is el kell végezni a keresést, majd az újonnan talált minimumot össze kell hasonlítani a már ott lévővel. Ennek eredményeként nyilvánvalóvá válik, hogy a 2 indexű háromszög a legközelebbi.

Most a "közeli" keresési algoritmusban használt köztes műveletek hatékony megvalósításáról szeretnék beszélni.

Ha szomszédot keres egy csomópontban, gyorsan ki kell számolnia egy pont és a háromszög közötti távolságot. Leírom a legegyszerűbb algoritmust:

Megtaláljuk az A pont vetületét (az a pont, amelyhez a legközelebbit keressük) a háromszög síkján. A talált pontot P-vel jelöljük. Ha P a háromszög belsejében van, akkor az A-tól a háromszögig mért távolság egyenlő az AP szakasz hosszával, ellenkező esetben megtaláljuk az A-tól a háromszög minden oldaláig (szakaszáig) mért távolságot. háromszög, válassza ki a minimumot. Probléma megoldódott.

A leírt algoritmus nem a leghatékonyabb. Egy hatékonyabb megközelítés egy olyan függvény keresésén és elemzésén alapul (a gradiens minimumának megtalálása stb.), amelynek értékei az összes lehetséges távolság egy adott ponttól a háromszög bármely pontjáig. A módszer meglehetősen nehezen érthető, és véleményem szerint külön cikket érdemel (eddig a kódomban volt implementálva, és lent találsz linket a kódra). A módszerrel a címen lehet megismerkedni. Ezt a módszert úgy találták 10-szer gyorsabb, mint amit korábban leírtam.

Egyszerű (3D) meghatározni, hogy egy O pontban középpontban lévő gömb R sugarú egy adott csomóponton belül van-e, amelyet határolókeret ábrázol:

Inline bool isSphereInBBox(const SBBox& bBox, const D3& pont, const double& sugár) ( return (bBox.m_minBB< point - radius && bBox.m_maxBB > < point - radius && bBox.m_maxBB >pont + sugár && bBox.m_minBB< point - radius && bBox.m_maxBB >pont + sugár); )
A gömb és a csomópont határoló dobozának metszéspontjának meghatározására szolgáló algoritmussal, a gömbön belüli csomópont vagy a csomóponton belüli gömb megtalálásával a dolgok némileg eltérőek. Ismét szemléltetem (a kép innen származik), és megadom a helyes kódot, amely lehetővé teszi ennek az eljárásnak a végrehajtását (2D-ben, 3D-ben hasonlóan):

bool metszi (KörTípus kör, RectType rect) ( circleDistance.x = abs(circle.x - rect.x); circleDistance.y = abs(circle.y - rect.y); if (circleDistance.x > (rect.width) /2 + circle.r)) ( return false; ) if (circleDistance.y > (rect.height/2 + circle.r)) ( return false; ) if (circleDistance.x<= (rect.width/2)) { return true; } if (circleDistance.y <= (rect.height/2)) { return true; } cornerDistance_sq = (circleDistance.x - rect.width/2)^2 + (circleDistance.y - rect.height/2)^2; return (cornerDistance_sq <= (circle.r^2)); }
Először (az első pár sor) csökkentjük a 4 kvadráns számításait egyre. A következő pár sorban ellenőrizzük, hogy a kör a zöld területen fekszik-e. Ha fekszik, akkor nincs kereszteződés. A következő néhány sor ellenőrzi, hogy a kör a rajz narancssárga vagy szürke területein van-e. Ha belép, akkor a kereszteződés megtalálható.

Valójában ez a számítás visszatér "hamis" minden olyan körre, amelynek középpontja a piros területen belül van, és "igaz" minden olyan körre, amelynek középpontja a fehér területen van.

Általában ez a kód biztosítja azt, amire szükségünk van (itt megadtam a kód 2D megvalósítását, de a KD-Tree kódomban a 3D verziót használom).

Még beszélni kell a keresési algoritmus sebességéről, valamint azokról a kritikus helyzetekről, amelyek lelassítják a keresést a KD-tree-ben.

Ahogy a fentiekben írják, "ventilátor" helyzetek nagyszámú elemet generálnak a csomóponton belül, minél több van belőlük, annál lassabb a keresés. Sőt, ha minden elem egyenlő távolságra van egy adott ponttól, akkor a keresés végrehajtásra kerül TOVÁBB)(a gömb felületén elhelyezkedő pontok halmaza, és a gömb középpontjához legközelebbi pontot keressük). Ha azonban ezeket a helyzeteket eltávolítjuk, akkor a keresés átlagosan egyenértékű lesz a fa leereszkedésével, több csomóponton lévő elemek felsorolásával, azaz. mögött O(log(N)). Nyilvánvaló, hogy a keresés sebessége a fa meglátogatott levélcsomópontjainak számától függ.

Tekintsük a következő két ábrát:

Ezeknek az ábráknak az a lényege, hogy ha az a pont, amelyhez a legközelebbi elemet keressük, nagyon-nagyon messze van a halmaz eredeti határolódobozától, akkor a gömb minDist (távolság a legközelebbitől) sokkal több csomópontot fog metszeni, mintha ugyanazt a gömböt tekintenénk, de a középpont sokkal közelebb van a halmaz eredeti határolókeretéhez (természetesen a minDist megváltozik). Általában egy távoli pont közelében történő keresés lassabb, mint az eredeti halmazhoz közeli pont keresése. A tesztjeim megerősítették ezt az információt.

Eredmények és összegzés

Befejezésül szeretnék még néhány szót fűzni a KD-Tree megvalósításához, és bemutatni az eredményeket. Valójában a kód kialakítását úgy fejlesztették ki, hogy könnyen adaptálható legyen az eredeti halmaz bármely objektumához (háromszögek, gömbök, pontok stb.). Csak egy osztályörököst kell létrehozni felülírt virtuális függvényekkel. Sőt, a megvalósításom egy speciális osztály teljesítését is előírja Splitter, amelyet a felhasználó határoz meg. Ez az osztály, vagy inkább a virtuális felosztási módszere határozza meg, hogy a vágási sík pontosan hol fog elhaladni. A megvalósításom során biztosítok egy osztályt, amely a SAH alapján dönt. Itt megjegyzem, hogy sok cikkben, amelyek egy SAH-alapú KD-fa felépítésének felgyorsításával foglalkoznak, sok szerző egyszerűbb technikákat használ a vágási sík megtalálására (például oszt a középponttal vagy mediánnal), és az SAH-heurisztikákat csak az a pillanat, amikor a csomópontban lévő elemek száma kicsi.

Az én implementációm nem tartalmaz ilyen trükköket, de lehetővé teszi ezek gyors hozzáadását (csak ki kell bővíteni a KD-Tree konstruktort egy új paraméterrel, és meg kell hívni a konstrukciós tag függvényt a kívánt elosztóval, szabályozva a szükséges korlátozásokat). Keresés egy fában, amit többszálon hajtok végre. Minden számítás dupla pontosságú számokkal történik. kettős). A maximális famélységet egy konstans adja meg (alapértelmezett -32). Néhány #meghatározza, lehetővé téve például a fán való bejárást rekurzió nélküli kereséskor (rekurzióval, bár gyorsabban lehet kilépni - minden csomópont valamilyen vektor eleme (vagyis a közelben található a memóriában), ami azt jelenti, hogy jól gyorsítótárazott) . A kóddal együtt tesztadatkészleteket adok ("megváltozott OFF formátumú" 3D modellek, amelyekben különböző számú háromszög található (2-től 3 000 000-ig)). A felhasználó kiírhatja a beépített fa kiíratását (DXF formátum), és megtekintheti a megfelelő grafikus programban. A program naplót is vezet (be- és kikapcsolható) a fa építési minőségéről: famélység visszaállítása, maximális elemszám egy levélcsomópontban, átlagos elemszám a levélcsomópontokban, futási idő. Semmi esetre sem állítom, hogy az így létrejött megvalósítás ideális, de mi van, én magam is ismerem azokat a helyeket, ahol kimaradtam (pl. nem adom át az allokátort a sablon paraméternek, a C-kód gyakori jelenléte ( Nem olvasok és nem írok fájlokat streamek segítségével), észrevétlen hibák is előfordulhatnak stb. – ideje kijavítani. És természetesen a fa szigorúan a 3D-s térben való munkára készült és optimalizált.

A kódot a következő jellemzőkkel rendelkező laptopon teszteltem: Intel Core I7-4750HQ, 4 mag (8 szál) 2 GHz, RAM-8 GB, Win x64 alkalmazás Windows 10 rendszeren. Az SAH I kiszámításához használt együtthatók a következők voltak: cT = 1., cI = 1,5. És ha már az eredményekről beszélünk, akkor ez kiderült 1,5 millió A háromszögfa kevesebb, mint 1,5 másodperc alatt épül fel. A 3 millió 2,4 másodperc alatt. Mert 1,5 millió pontok és 1,5 millió háromszögek (a pontok nem túl messze vannak az eredeti modelltől), a keresés 0,23 másodperc alatt fejeződött be, és ha a pontokat eltávolítják a modellből, az idő megnő, akár 3 másodpercig. Mert 3 millió pontok (ismét a modell közelében találhatók) és 3 millió A háromszögek keresése körülbelül 0,7 másodpercet vesz igénybe. Remélem nem kevertem össze semmit. Végül egy illusztráció a megszerkesztett KD-fa vizualizációjáról:

Tekintsük a kd nevű bináris térbeli partíció szerkezetét -faipari. Ez a struktúra egymásba ágyazott határoló dobozok bináris fája. Mindegyik paralelepip befelé kd -fát az egyik koordinátatengelyre merőleges sík osztja két gyermekparallepipedonra.

Az egész jelenet teljes egészében a gyökérdobozban van, de folytatva a dobozok rekurzív particionálását, arra a következtetésre juthatunk, hogy minden levéldoboz csak kis számú primitívet tartalmaz. És így, kd A -tree lehetővé teszi a bináris keresés használatát a sugár által metszett primitív megkeresésére.

Kd fa építése

A kd-fa létrehozásának algoritmusa a következőképpen ábrázolható (a téglalap alakú dobozt az angol "box" (doboz) szóval fogjuk nevezni).

Az összes primitív "hozzáadása" a határoló dobozhoz. Ez azt jelenti, hogy minden primitívet határoló dobozt kell építeni, amely megfelel a fa gyökércsomópontjának.

Ha kevés primitív van a csomópontban, vagy elérte a fa mélységi határát, állítsa le az építést.

Válasszon ki egy osztott síkot, amely az adott csomópontot két gyermekre osztja. Nevezzük őket a fa jobb és bal csomópontjának.

Adja hozzá a bal oldali csomópontdobozt metsző primitíveket a bal csomóponthoz, a jobb oldali csomópontdobozt metsző primitíveket a jobb csomóponthoz.

A kd-fa felépítésében a legnehezebb a 3. lépés. A gyorsító szerkezet hatékonysága közvetlenül attól függ. A partíciósík kiválasztásának többféle módja van, nézzük ezeket sorrendben.

1. Válassza ki a hasítósíkot középen.

A legegyszerűbb, ha a doboz közepén egy síkot választunk. Először válassza ki azt a tengelyt (x, y vagy z), amelyben a doboz a maximális méretet képviseli, majd ossza fel a dobozt középen.

Kép 1 : Osztott középpont

Ennek a módszernek gyenge az alkalmazkodóképessége. A klasszikus oktrának ugyanazok a hátrányai. Intuitív módon az ilyen fákon tapasztalható gyenge sebesség okát azzal írhatjuk le, hogy minden csomóponton sok üres hely van, amelyen a sugár áthalad (a keresés során áthalad a fán), míg az üres helyet el kell hagyni lehető leghamarabb. A szigorúbb magyarázatot kicsit később adjuk.

2. Válassza ki a síkot medián szerint.

Azt gondolhatnánk, hogy jó lenne minden alkalommal két gyermekre osztani a csomópontot, hogy a primitívek száma a jobb és a bal részfában azonos legyen. Ily módon egy kiegyensúlyozott fát építünk, ami felgyorsítja a keresést.

2. ábra : Medián szerint osztva

Ez nem túl jó ötlet. A helyzet az, hogy a kiegyensúlyozott fák csak akkor tudnak segíteni, ha a kívánt elem minden alkalommal egy véletlenszerű csomóponton található, vagyis ha a sugarak eloszlása ​​a csomópontokon a keresés során egyenletes. A valóságban nem az. Átlagosan több sugár fog eljutni ahhoz a csomóponthoz, amely felülete nagyobb, és egy medián partícióval a csomópontok ezen területei eltérőek lehetnek.

3. Felületi heurisztikus (SAH)

Mik a jól felépített kd-fa kritériumai? Intuitív szinten ez valójában nem túl világos, bár a "lehetőleg minél több fehér területet a lehető leggyorsabban el kell dobni" kifejezés valószínűleg megfelelne.

Formális megközelítést alkalmazunk. Bemutatjuk a költségbejárási függvényt, amely megmutatja, hogy a számítási erőforrások szempontjából mennyire költséges egy adott csomópontot véletlenszerű sugárkészlettel követni. A következő képlet segítségével számoljuk ki.

SAH(x) = CostEmpty + Felületi terület (bal)*N (bal) + Felületterület (jobb) * N (jobb)

Ahol a CostEmpty egy üres csomópont nyomon követésének költsége (valamilyen állandó), a SurfaceArea a megfelelő csomópont felülete, N pedig a benne lévő primitívek száma. A felosztási síkot úgy kell megválasztani, hogy ez a funkció minimális legyen. Az x függvény argumentuma a partíciósík egydimenziós koordinátája.

A primitív korlátok jó jelöltek egy minimális SAH-ra. Egy egyszerű építési algoritmus így néz ki. Minden alkalommal, amikor kiválaszt egy síkot, három dimenzióban át kell mennie a primitívek összes lehetséges határán, ki kell számítania bennük a költségfüggvény értékét, és meg kell találnia ezen értékek közül a minimumot. Amikor minden síkra kiszámítjuk az SAH-t, tudnunk kell N(bal) és N(jobbra) - a síktól jobbra és balra lévő primitívek számát. Ha egyszerű felsorolással kiszámítjuk N-t, akkor egy négyzetes bonyolultságú konstrukciós algoritmust kapunk.

Kép 3 : Partícionálás SAH-val

A 4. ábrán látható, hogy az SAH azonnal eldobja a nagy üres helyeket, szorosan korlátozva a geometriát.

Kép 4 : kd-fa SAH szem előtt tartásával készült

A felületi heurisztika intelligensebb leállítási feltételeket generál, mint egy famélység-korlát vagy néhány primitív. Ha a kiválasztott osztott síkon az utódcsomópontok nyomon követésének teljes költsége nagyobb, mint az aktuális csomópont levélként való nyomon követésének költsége (azaz Felületterület(Csomópont)*N(Node)), akkor a faépítést le kell állítani.

4. Kd fa gyors felépítése

0. lehetőség

Középen felosztva válassza ki azt a tengelyt, amely mentén a doboz mérete a legnagyobb. Ez a módszer a leggyorsabb, de egyes jelenetekben a sugárkövetés egy ilyen fában körülbelül 2-3-szor lassabb.

1.opció

Az építkezés felgyorsítása érdekében a legegyszerűbb dolog az iterált síkok számának csökkentése. Ahelyett, hogy N síkon iterálnánk (ahol N a primitívek száma), az SAH csak kis számú előre rögzített helyen számítható ki. A beviteli mező minden tengely mentén egyenletesen van felosztva M részre. Általában M néhány tíz és néhány száz közötti tartományba esik. N(bal) és N(jobb) még mindig iterációval kerül kiszámításra, de most már csak M-szer kell iterálnunk a tömböt, N-t nem. Így az algoritmus N*M komplexitást kap. Valójában a gyorsítást az SAH diszkretizálásával való durvításával értük el. Kiderült azonban, hogy a kapott durva függvény minimumának értéke általában nem sokban tér el a pontos minimumától.

2. lehetőség

Mit lehet tenni az 1. lehetőség felgyorsítása érdekében? N(bal) és N(jobb) számítása során meg kell szabadulnunk a kimerítő kereséstől. Ehhez készítünk egy fát, amelynek minden csomópontja tartalmaz valamilyen hasítósíkot és a síktól jobbra és balra lévő primitívek számát. structIntervalTree

úszó hasított;

int numPrimsOnLeftSide;

int numPrimsOnRightSide;

IntervalTree* balra;

Interval Tree*jobbra;

Valójában három ilyen fára van szükségünk minden szinten – egy x, y, z számára. A beviteli intervallum minden alkalommal felére lesz osztva. Egy ilyen fa birtokában log(N) műveletekben pontosan meghatározható a síktól jobbra és balra lévő primitívek száma. A keresési algoritmus a fában meglehetősen egyszerűnek tűnik.

vec2i IntervalTree::TraversePlane(

úszó a_split) const

// a minimumot a nulla komponensben fogjuk tárolni, a maximumot az elsőben

vec2i res; // két egész szám vektora

ha(a_split< split - EPSILON)

res = numPrimsOnRightSide;

ha(balra!=0)

res += Bal()->TraversePlane(a_split);

// Számolja meg legalább azokat a primitíveket, amelyek ebben a csomópontban vannak, hogy a SAH ne legyen nulla.

Ha(res.M == 0)

res.M = numPrimsOnLeftSide;

Másha(a_split > split + EPSILON)

res = numPrimsOnLeftSide;

Ha(jobbra!=0)

res += jobb->TraversePlane(a_split);

// ha valamiért a primitívek száma nulla, akkor

// Számolja meg legalább azokat a primitíveket, amelyek ebben a csomópontban vannak, hogy a SAH ne legyen nulla.

Ha(res==0)

res = numPrimsOnRightSide;

Más

// pontosan eltalálja a csomópont síkját

res = numPrimsOnLeftSide;

res = numPrimsOnRightSide;

Visszatérés res;

A síkfa felépítésének bonyolultsága N*log(N). Az SAH becslésének bonyolultsága M*log(N), mivel az SAH-t csak M fix síkban számoljuk. Így az algoritmus teljes komplexitása N*log(N), mert M sokkal kisebb, mint N.

A kd fa felépítése előtt elvileg tetszőleges gyorsító szerkezetet készíthetünk, csak hogy a későbbiekben felgyorsítsuk az SAH számítását.

3. lehetőség (Majdnem pontosan és N*Log(N))

Rendezést használunk. Minden tengelyhez (x,y,z) rendezze a primitíveket először a maximumok, majd a határolókeretek minimumai szerint. Nevezzük a maximumok szerint rendezett tömböt sorted_max-nak. Tömb minimum szerint rendezve - sorted_min.

A sorted_min tömbön balról jobbra haladva minden alkalommal pontosan tudjuk, hogy hány primitív (vagy inkább határoló doboza) van a síktól jobbra (és szinte pontosan tudjuk, hogy hány primitív van balra). A sorted_max tömböt jobbról balra haladva pontosan tudjuk, hogy hány primitív fekszik a sík bal oldalán, és majdnem pontosan hány a jobb oldalon.

számára(inttengely = 0; tengely < 3; tengely++)

// A rendezési primitívek az aktuális tengelyhez és a min határokhoz tartoznak

// ÖsszehasonlításMinösszehasonlító(tengely); std:: fajta(prims. kezdődik(), prims. vége(), összehasonlító); számára(intén=1; én< prims. méret(); én++) intonLeftSide = én; intonRightSide = prims. méret()- én; úszóhasított = prims[ én]. Doboz(). vmin[ tengely]; ha(hasított == egy doboz. vmin[ tengely]) folytatni;

// SAH kiértékelése

AABB3fbox_left = egy doboz;

AABB3fbox_right = egy doboz;

Box_left. vmax[ tengely] = hasított;

Box_right. vmin[ tengely] = hasított;

úszósah=EMPTY_COST+ onLeftSide* felszíni terület(box_left) + onRightSide* felszíni terület(box_right);

Ha (sah < min_sah)

Min_sah = sah;

Min_split = hasított;

min_tengely = tengely;

// A rendezési primitívek az aktuális tengelyhez és a max korlátokhoz tartoznak

// ÖsszehasonlításMaxösszehasonlító2(tengely); std:: fajta(prims. kezdődik(), prims. vége(), összehasonlító2); számára(intén= prims. méret()-2; én>=0; én--) intonLeftSide = én+1; intonRightSide = prims. méret()- én-1; úszóhasított = prims[ én]. Doboz(). vmax[ tengely]; ha(hasított == egy doboz. vmax[ tengely]) folytatni;

// SAH kiértékelése

AABB3f box_left = egy doboz;

AABB3f box_right = egy doboz;

Box_left.vmax[tengely] = hasított;

Box_right.vmin[tengely] = hasított;

úszó sah=EMPTY_COST+ onLeftSide*felszíni terület(box_left) + onRightSide*felszíni terület(box_right);

Ha (sah < min_sah)

Min_sah = sah;

Min_split = hasított;

min_tengely = tengely;

Elméletileg a módszerrel van egy probléma. Tekintsük a sorted_min tömböt. Lapozd át balról jobbra:

for (int i=0;i méret();i++)

onLeftSide = én;

int onRightSide = prims.méret()-én;

// ...

Az onLeftSide számát teljesen pontosan tudjuk, de az onRightSide számát nem egészen. A helyzet az, hogy a sík feloszthat néhány primitívet, és ebben az esetben ugyanaz a primitív fekszik a síktól jobbra és balra is, amit ez az algoritmus nem vesz figyelembe. A gyakorlatban ez a probléma gyakorlatilag nem jelentkezik.

4. lehetőség

Az SAH függvény minimumának keresését felgyorsíthatja valamilyen minimalizálási módszerrel, több kezdeti közelítéssel. Mondjuk az aranymetszet módszerét. Ilyenkor a kimerítő keresési módszertől is megszabadulunk. Csak azt kell figyelembe venni, hogy az SAH többé-kevésbé sima formát csak nagyszámú primitívvel nyer. Ennek a megközelítésnek az az előnye, hogy az SAH nyers erővel történő kiszámítása könnyen áthelyezhető a GPU-ra. Ezért minden alkalommal, amikor az SAH-t nyers erővel becsüljük meg, és a becslések számát kis számra csökkentjük (max. 10-20), ezzel a módszerrel nagyon gyorsan fel lehet építeni egy kd-fát.

5. lehetőség (Binning)

Ezt a lehetőséget gyakran használják. A lényeg a következő:

A teret fel kell osztani x, y és z szabályos intervallumokra. Minden ilyen intervallumot bin-nek nevezünk. Általában kis számú kosárra korlátozódik ~32.

A háromszögek középpontját kivesszük és kosarakba helyezzük. Ez azt jelenti, hogy át kell mennie az összes háromszögön, és ki kell számítania a középpontjukat. Ezt követően minden kosárnál ki kell számolni, hogy hány pont (közép) esett bele. Könnyű megtenni. A középpont kiszámításakor csak növelnie kell a megfelelő számlálót. Mivel a kosarakra való felosztás szabályos, egy pont koordinátája birtokában azonnal meghatározható, hogy melyik kosárba esik.

Sugárkövetés a kd-tree-ben a CPU-n

innen töltheti le az algoritmust

A klasszikus bináris keresési algoritmus kd fákban (az angol szakirodalomban kd-tree traversal), amelyet a legtöbb CPU megvalósításai a következők.Az algoritmus első lépésében ki kell számítani a sugár és a jelenetet határoló gyökérdoboz metszéspontját, és el kell tárolni a metszéspontra vonatkozó információkat két koordináta formájában (a sugár terében) - t_közel és t_távol , amely a közeli és távoli síkkal való metszéspontot jelöli. Minden következő lépésben csak az aktuális csomópontról (annak címéről) és erről a két koordinátáról van szükség információra.

Ebben az esetben nem kell kiszámolni a sugár és a gyermekdoboz metszéspontját, elég megtudni a metszéspontot a dobozt szétválasztó síkkal (a megfelelő koordinátát jelöljük t_split ). Minden nem levél csomópont kd a fának két gyermek csomópontja van. ábrán Az 5. a sugár útjának nyomon követése során előforduló események három változatát mutatja be.

5. ábra : Sugár nyomkövetése kd fában

Mikor A (t_split >= t_távol) vagy B (t_split< t_near) a sugár csak egy gyermek csomópontot metsz, így egyszerűen eldobhatja a jobb (illetve bal) csomópontotés folytassa a kereszteződés keresését a fennmaradó csomópontnál.

Mikor C a sugár metszi mindkét gyermek csomópontot, ezért először a közeli csomópontban kell metszéspontot keresni, és ha nem található, akkor a távoliban. Mivel általában nem ismert, hogy az utolsó esemény hányszor fog bekövetkezni, veremre van szükség. Minden alkalommal, amikor egy sugár áthalad mindkét gyermek csomóponton, a távoli csomópont címe, t_közel és t_távol a verembe tolják, és a keresés a közelben folytatódik. Ha nem található metszéspont a legközelebbi csomópontnál, a távoli csomópont címe kikerül a veremből, t_közel, t_távol és a keresés a távoli csomóponton folytatódik.

Sugárkövetés a kd-tree-ben GPU-n

A GPU óta kezdetben nincs verem, megjelentek a verem nélküli algoritmusok és a kis hosszúságú mesterséges vermet használó algoritmusok. A GPU öt algoritmus ismert a sugár útjának követésére -újraindítás, visszalépés, lenyomás, short stack és a nyomkövetési algoritmus kd fa linkekkel.

kd fa újraindítása

Kép 2 : művelet újraindítási algoritmusa.

Ha a sugár nem talál metszéspontot egy levélben, a t_far értéke t_near lesz, és a keresés a kd fa gyökerétől folytatódik (2. ábra). Nagyjából elmondható, hogy a sugár origója egyszerűen elmozdul - vagyis a kibocsátási pontja, és a keresés kezdődik elölről. Ez azt eredményezi, hogy a sugár sokszor áthalad ugyanazokon a csomópontokon, ami nem hatékony.

kd-tree push-down

Enyhe módosításújrakezd algoritmus, ami abból áll, hogy a sugár nem a fa gyökeréből indul ki, hanem valamilyen részfából. Egy csomópontot azonban csak akkor lehet új részfának választani, ha a teljes leszállás alatt nem volt egyetlen olyan csomópont sem, amelyben a sugár mindkét gyermekcsomópontot metszi.

Vagyis ha a legközelebbi csomópontok leereszkedésekor kd fa legalább egyszer találkozott olyan csomóponttal, amelyben a sugár a közeli és távoli gyermekcsomópontot is metszi, akkor ezt a távoli gyermekcsomópontot kell részfaként kiválasztani. Továbbá, ha a sugár kimaradt, az újraindítás a megjegyzett távoli csomópontról történik, és ismét megpróbálhat új részfát keresni. Valójában ez egy kísérlet egy 1 elem hosszúságú verem létrehozására.

kd fa short stack

A szerzők a short stacket is használták. Amíg a verem mérete elegendő, a klasszikus algoritmushoz hasonlóan töltjük ki. Amikor a verem túlcsordul, gyűrűpufferként kezd működni. Ha a verem üres, újra kell indítani. Például, ha egy 4 hosszúságú verem (1), (4), (6), (8) csomópontokat tartalmaz, akkor új elem (12) hozzáadásakor a verem így fog kinézni: (12) , (4), (6), (8). Vagyis az első elem felülírásra kerül. Az elemek a hozzáadás sorrendjében kerülnek eltávolításra (azaz először 12, majd 8, 6 és végül 4), de amikor az elemet (4) eltávolítjuk a veremből, újra kell indítani, mivel töröltük az (1) elemet. A short stack lényege, hogy nagymértékben csökkenti az újraindítások számát, amit egy sugárnak meg kell tennie.

kd-tree backtrack

Ha csomópontokban tároljuk kd fa egy hivatkozást a szülő csomópontokhoz, ha ezt a hivatkozást kihagyja, elérheti a szülőt. Ezenkívül minden csomóponton el kell tárolni a határoló dobozát, hogy újat tudjunk számítani t_far kihagyás esetén.

Ct_near ugyanazt teheti, mint az esetbenújrakezd algoritmus. Ehhez további 6*4 (a téglatest koordinátákhoz) + 4 (a szülőhivatkozáshoz) = 28 bájt szükséges. Az emlékezet óta GPU meglehetősen korlátozott, az ilyen hulladék problémákat okozhat. Ezen kívül minden egyes emeléskor ki kell számítani a nyaláb és a tengelyek mentén elhelyezkedő paralelipipid metszéspontját, ami természetesen nem ingyenes a számítási erőforrások szempontjából. Külön meg kell jegyezni, hogy egy megőrzött téglatestű kd fa sokkal több memóriát foglal el, mint egy jól felépített BVH fa ugyanabban a jelenetben. Ennek fő oka az, hogy a kd fában a téglatesteknek több közös pontja lesz, ami a végén megkettőződik.

kd-fa kötegekkel

Ebben a változatban minden csomópont kd fa, hat hivatkozást adunk a fa szomszédos csomópontjaihoz (azokhoz a csomópontokhoz, amelyek ezt a csomópontot érintik) (3. ábra). Ha a sugár kihagyja az aktuális csomópontot, akkor a kötegek segítségével eljuthatunk a következő csomópontokhoz, ahol a sugarat nyomon kell követni.

Ez az algoritmus pl visszalép elkerüli ugyanazon fa csomópontjainak többszöri bejárását. Mindazonáltal hat link további 24 bájt memóriát igényel, ami 32 bájtot ad a meglévő 8 bájthoz.

Kép 3 : kd fa kötegekkel .

A kd fák előnyei

1. Egy nagyon egyszerű és hatékony bejárási algoritmus. Még a GPU-hoz is.
2. Kevés memóriát foglalnak el (8 bájt csomópontonként).

A kd fák hátrányai

Időigényes konstrukció, nevezetesen minimális SAH-val rendelkező partíció keresése.

Mélyebb, mint a BVH. További építési lépések.

Következtetés

Összefoglalva, a kd fa ideális sugárkövetéshez. Ez igaz a CPU-ra és a GPU-ra is.

Irodalom

Wald I. Valós idejű sugárkövetés és interaktív globális megvilágítás. PhD dolgozat, Saarlandi Egyetem, 2004.

1. Sevcov M., Soupikov A., Kapustin A.

   Nagyon párhuzamosan gyors KD-fa konstrukció a dinamikus jelenetek interaktív sugárkövetéséhez. In Proceedings of the EUROGRAPHICS konferencia, 2007.

Foley T., Sugerman J . KD-Tree gyorsítási struktúrák egy GPU Raytracerhez. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Conference on Graphics hardver, p. 2005. 15-22.

Horn D., Sugerman J., Houston M., Hanrahan P. Interactive k-D Tree GPU Raytracing. Az interaktív 3D grafikákról és a gyors renderingről szóló játékokról szóló szimpózium anyaga, p. 167-174, 2007.

Popov S., Günther J., Seidel H.-P., Slusallek P. Stackless KD-Tree Traversal for High Performance GPU Ray Tracing. In Proceedings of the EUROGRAPHICS konferencia, 2007.

– adatstruktúra, amely egy fastruktúra, amely összekapcsolt csomópontok halmazából áll.

Ez egy véges elemhalmaz, amely vagy üres, vagy tartalmaz egy elemet (gyökér) két különböző bináris fához, ún. bal és jobb részfa. A bináris fa minden elemét csomópontnak nevezzük. A fa csomópontjai közötti kapcsolatokat ágainak nevezzük.

A bináris fa ábrázolásának módja:

• A - fagyökér
• B a bal oldali részfa gyökere
• C a jobb oldali részfa gyökere

A fa gyökere a minimális érték szintjén található.

Azt a D csomópontot, amely közvetlenül a B csomópont alatt van, B gyermekének nevezzük. Ha D az i szinten van, akkor B az i-1 szinten van. A B csomópontot D ősének nevezzük.

A fa bármely elemének maximális szintjét mélységének vagy magasságának nevezzük.

Ha egy elemnek nincsenek gyermekei, akkor levélnek, ill terminál csomópont fa.

A fennmaradó elemek belső csomópontok (elágazó csomópontok).

Egy belső csomópont gyermekeinek számát fokának nevezzük. Az összes csomópont maximális foka a fa foka.

A gyökértől az x csomópontig tartó ágak számát az x-hez vezető út hosszának nevezzük. A gyökér úthossza 0; az i szinten lévő csomópont úthossza egyenlő i -vel.

A bináris fát olyan esetekben használjuk, amikor a számítási folyamat minden pontján két lehetséges döntés egyikét kell meghozni.

A fán sok feladatot el lehet végezni.

Gyakori feladat egy adott p művelet végrehajtása a fa minden elemén. Itt p-t az összes csomópont meglátogatásával kapcsolatos általánosabb probléma vagy a fa bejárási probléma paraméterének tekintjük.

Ha a feladatot egyetlen szekvenciális folyamatnak tekintjük, akkor az egyes csomópontok meghatározott sorrendben látogathatók, és lineárisan helyezkednek el.

Fa bejárási módszerek

Legyen egy fa, ahol A gyökér, B és C bal és jobb részfa.

Háromféleképpen lehet áthaladni egy fán:

• Fa bejárás fentről lefelé (közvetlen sorrendben): A, B, C - előtag forma.
• Fa bejárás szimmetrikus sorrendben (balról jobbra): B, A, C - infix forma.
• Fa bejárás fordított sorrendben (alulról felfelé): B, C, A - postfix forma.

Fa megvalósítás

A fa csomópontja struktúraként írható le:

struct tnode(

terület; // adatmező

Struktúra csomópont *jobbra; // helyes gyerek
};

Ebben az esetben a fa bejárása előtag formájában így fog kinézni

if (fa!=NULL) (

cout<< tree->terület; //A fa gyökerének megjelenítése

A fa bejárása infix formában így fog kinézni

void treeprint(tnode *fa) (

if (fa!=NULL) ( //Amíg egy üres csomópont nem találkozik

cout<< tree->terület; //A fa gyökerének megjelenítése

A fa bejárása postfix formában így fog kinézni

void treeprint(tnode *fa) (

if (fa!=NULL) ( //Amíg egy üres csomópont nem találkozik

cout<< tree->terület; //A fa gyökerének megjelenítése

Bináris (bináris) keresőfa egy bináris fa, amelyre a következő további feltételek (keresési fa tulajdonságai) teljesülnek:

• mindkét részfa, bal és jobb, bináris keresőfa;
• egy tetszőleges X csomópont bal oldali részfájának összes csomópontjának adatkulcsértéke kisebb, mint magának az X csomópont adatkulcsának értéke;
• egy tetszőleges X csomópont jobb oldali részfájának összes csomópontjának adatkulcsértéke nem kisebb, mint az X csomópont adatkulcsértéke.

Az egyes csomópontokon lévő adatoknak kulcsokkal kell rendelkezniük, amelyeken a kisebb, mint összehasonlítás művelet definiálva van.

Az egyes csomópontokat reprezentáló információ általában egy rekord, nem pedig egyetlen adatmező.

Bináris keresési fa összeállításához fontolja meg egy csomópont hozzáadásának funkcióját a fához.

Csomópontok hozzáadása a fához

struct tnode * addnode(int x, tnode *fa) (

Ha (fa == NULL) ( // Ha nincs fa, akkor a gyökeret képezzük

fa=új csomópont; // memória a csomóponthoz

fa->mező = x; // adatmező

fa->bal = NULL;

fa->jobbra = NULL; // az ágak ürességgel inicializálódnak

)else if (x< tree->terület) // bal oldali gyermek hozzáadásának feltétele

fa->bal = addnode(x,fa->bal);

Más // a megfelelő gyermek hozzáadásának feltétele

fa->jobb = addnode(x, fa->jobb);

visszatérés(fa);
}

Egy részfa eltávolítása

void freemem(tnode *fa) (

Ha (fa!=NULL) (

freemem(fa->bal);

freemem(fa->jobb);

fa törlése;

Példa Írjon programot, amely megszámolja a szavak előfordulási gyakoriságát a bemeneti adatfolyamban.

Mivel a szavak listája nem ismert előre, nem tudjuk előrendelni. Nem bölcs dolog lineáris keresést használni minden egyes kapott szóra annak megállapítására, hogy korábban előfordult-e vagy sem, mert ebben az esetben a program túl lassan fut.

Az egyik módja a már beérkezett szavak sorrendjének folyamatos fenntartása, minden új szót olyan helyre helyezve, hogy a meglévő sorrend ne sérüljön. Használjunk bináris fát.

A fában minden csomópont a következőket tartalmazza:

• mutató a szó szövegére;
• előfordulási szám számláló;
• mutató a bal oldali gyermekre;
• mutat a megfelelő gyerekre.

Tekintsük a program végrehajtását a kifejezés példáján

A fa így fog kinézni:

Megvalósítási példa

#beleértve
#beleértve
#beleértve
#beleértve
#define MAXWORD 100
struct tnode ( // fa csomópont

Char*szó; // mutató a karakterláncra (szó)

int count; // előfordulások száma

Struct tnode *bal; // bal gyerek

Struktúra csomópont *jobbra; // helyes gyerek
};
// Funkció csomópont hozzáadására a fához
struct tnode *addtree(struct tnode *p, char *w) (

A bejegyzés eleje a változtatás kedvéért a "Seryozha, te matekot tanulsz! Írj szigorúan" szellemében, ne figyelj, akkor minden rendben.
Igen, és nem úgy értettem, hogy sok tapasztalatom van ebben a témában, hanem elég kevés, de megkérték, hogy mondjam el.

Tegyük fel, hogy van egy halmazunk az X lehetséges elemeiből, az A kiválasztott részhalmaza, és a feladat az, hogy az X-ből adott x-ből hány „leghasonlóbb” az A-ban. Például a tíz „leghasonlóbb”. Vagy mindenki, akinek a "hasonlósága" nem kisebb, mint egy adott. Kívánatos, hogy ne válogatja az összes A-t, ez hosszú idő.

A feladat kiváló, és ami a legfontosabb, gyorsan megoldható, ha az elemek számok, és minél nagyobb a "hasonlóság", minél közelebb vannak egymáshoz az értékek: csak egy rendezett tömb és egy bináris keresés, vagy egy keresőfa. (bináris, n-áris, B-fa -- nem számít).

Ami ebben az esetben lehetővé teszi a probléma gyors megoldását: a készleten adott parancs jelenléte, összhangban a „hasonlósággal”. Vagyis ha a kívánt x elem< a, и a < b, то x более похож на a, чем на b. Это позволяет не рассматривать сильно большие/меньшие элементы, так как они заведомо хуже подходят.

Ha a "hasonlóságot" másképpen definiálja, például a tizedesjegyek Levenshtein-távolságán keresztül, a sorrend jelenléte már nem segít. Vagyis pont az egyiknek a másikkal való összhangjában van a lényeg, és nem abban, hogy a sorrendet legalább valahogy be tudjuk állítani, főleg, hogy "legalább valahogy" mindig lehetséges, van ilyen tétel a halmazelméletben.

A probléma az, hogy nem mindig van megfelelő rendelés. A fő feladat, amelyről még lesz szó: az elemek pontok a síkon, és minél nagyobb a hasonlóság, minél kisebb a távolság a pontok között.

Egy n-dimenziós tér esetén mind a probléma, mind a megoldások triviálisan általánosítva vannak, és úgy tűnik, még egy kicsit tovább is lehet menni, erről lentebb.

Ötletek

Az első gondolat, ami egy normális embernek eszébe jut, aki nem akar valami bonyolultat kitalálni: "bontsuk sejtekre". Vagyis a síkot négyzetekre osztják, a rendelkezésre álló pontokat a megfelelő négyzetekhez kötik, a négyzetet, amelyben fekszik, az x pont határozza meg, a keresést ezen és több szomszédoson hajtják végre. Nem működik túl jól. A probléma az, hogy ez egy "adatfüggetlen" particionálási módszer, emiatt nagyon egyszerű, ettől fogva nagyon rosszul tud illeszkedni egy adott ponthalmazhoz. Például, ha kiderült, hogy a pontok 99%-a egy cellában összpontosul, akkor is át kell válogatni mindent, és nagyon igyekeztünk.

Második gondolat: és akkor tegyük gyakoribbá a cellákat azokon a helyeken, ahol több pont van. Gyerünk. Ezek csak fél intézkedések, vigyük a végére az ötletet:

• Egy nagy cellával kezdjük.


• Ha egy cellában túl sok a rendezendő pont, akkor azt két részre osztjuk. Annak érdekében, hogy a cellákhoz könnyebb legyen pontokat rendelni, felosztjuk őket például függőleges és vízszintes vonalakkal, felváltva erre-arra (az külön kérdés, hogy pontosan hol kell megrajzolni).


• Kövesse az előző bekezdést, amíg az összes cella megfelelő számú pontot nem kap

Az eredmény egy nyilvánvaló hierarchikus felépítés: a legfelső szintű cellák két kisebb cellát (jobb és bal vagy felső és alsó), a levélsejtek pontokat tartalmaznak. Ez egy kétdimenziós KD-fa (a K-dimenziósból, azaz K-dimenziósból), egy bináris fa általánosítása többdimenziós térre. Ha a méret kettőnél nagyobb, az egyenesek helyett a koordinátatengelyekre merőleges síkok (hipersíkok) lesznek. A fő gondolat, remélem, világos.

Harmadik gondolat: miért kellenek olyan cellák ahol nincs pont, csak ott építsünk cellákat, ahol szükséges. Nem lehetett olyan röviden és egyértelműen leírni, mint egy KD-fát, de valami ilyesmit:

• Nincsenek pontok, nincsenek cellák.


• Az első pont megjelenésével egy téglalap épül körülötte pontosan méretben (0x0 oldallal).


• Folytatjuk a pontok egyenkénti hozzáadását, szükség szerint bővítve a téglalapot. Az oldalak párhuzamosak a tengellyel, ami leegyszerűsíti a találati pontok kiszámítását. Nevezzük továbbra is a „téglalapot” „csomónak”.


• Ha túl sok pont van egy csomópontban, a struktúra átalakul:
  • megjelenik egy gyökér, amely maga nem tartalmaz pontokat, hanem gyermek csomópontokat tartalmaz
  
  
  • és az eredeti csomópont több részre oszlik (hát pl. kettőre), és ezek mind a gyökér gyermekeivé válnak


• A pontok folyamatosan bővülnek. Ha egy új pont közvetlenül egy meglévő csomópontban található, akkor hozzáadódik hozzá, ha nem, akkor azt a csomópontot választja ki, amelynek kisebb területet kell növelnie, mint másoknak, hogy új pontot tartalmazzon (az ötlet az, hogy minél kisebb a teljes terület a csomópontok, annál jobb az eredmény).


• A csomók folyamatosan szétesnek. Amikor a következő csomópont túlcsordul, az szétesik, és mindannyian a gyökér gyermekeivé válnak.


• Amíg nincs túl sok csomópont a gyökérben. Ezután maga a gyökér részekre bomlik, amelyek az új gyökér gyermekeivé válnak. Minden ilyen részhez tartozik egy téglalap, amely tartalmazza az összes gyermekét, és szükség szerint bővül.


• És így tovább, amíg az összes pontot hozzáadjuk

Ezt R-fának hívják (az R a téglalapot jelenti), a B-fa általánosítása többdimenziós esetre. Ha kettőnél több dimenzió van, akkor n-dimenziós paralelepipedonokat kapunk. Talán észrevetted, hogy az építés során kiderülhet, hogy a különböző csomópontok metszik egymást; nem kritikus, bár kellemetlen. Ismét remélem, hogy néhány általános elképzelés világos.

Hogyan kell keresni

Lesz pár szó a faépítés okairól. De miután mindent felépítettünk, kiderül, hogy a KD-fa csak egy speciális esete az R-fának: minden csomópont csak két következő szintű csomópontot tartalmaz, és a térben ezek nagyon meghatározott módon helyezkednek el, de minden ez az R-fák megengedett határain belül van, és nincs más eltérés. Tehát a legközelebbi pontok megtalálásának algoritmusa általánosként írható fel. Valami ilyesmi:

Van egy működő implementációm, elég gyorsan működött (egy brute-force kereséshez képest), de nagyon régen írták, és most nem igazán tetszik a kód. Túl lusta megjavítani. Szóval ami lent van, az kiment a fejemből, el sem kezdődött. Legyen óvatos.

1. feladat: keresse meg az összes pontot, amely legfeljebb R távolságra van x-től
A belső csomópontok esetében a gyermekek csomópontok:
def getBall(self, x, R): return sum(, )
A levelek esetében a gyerekek pontok:
def getBall(self, x, R): return sum(, )
Ha szeretné, természetesen meghatározhat egy getBall() függvényt a pontokhoz, és törölheti a levelek és a gyökerek közötti különbséget ezen a ponton.

2. probléma: keresse meg az x-hez legközelebbi n pontot
Először is létre kell hoznia egy prioritási sort, amely úgy van elrendezve, hogy az x-től legtávolabbi pont legyen felül, és az elsőként lépjen ki. A szabványos Python heapq nem teszi lehetővé az összehasonlító függvény megadását (vagy nem vagyok tisztában, és valahogy egyszerűen és szépen le tudod cserélni a "kevesebb, mint" operátort bizonyos esetekben, vagy a fejlesztők nem igazán gondolj a felületre), úgy látszik valami más kell, inkább csak valaki már írt. Legyen ilyen, ez a q paraméterben kerül átadásra. Aztán valami ilyesmi:

Belső csomópontokhoz:
def getN(self, x, q, n): self.children.sort(key = lambda a, x=x: a.dist(x)) # mindegy, milyen sorrendben jönnek a gyerekek, rendezd. c-nek önmagában.gyerekek: if (len(q)< n) or q.top.dist(x) >c.dist(x): # ha vannak még teljesen üres helyek, q = c.getN(x, q, n) # vagy van esély a jelenlegi legrosszabbnál közelebbi ponttal találkozni: törd # mert csak rendezett gyerekek, csak rosszabb lesz vissza q
A levelekhez:
def getN(self, x, q, n): self.children.sort(lambda a,x=x: a.dist(x)) # nem számít, milyen sorrendben jönnek a gyerekek, rendezd c-re önmagában .childs: if (len(q)< n) or q.top.dist(x) >c.dist(x): # ha még vannak üres mezők, q.push(c) # vagy egy pont közelebb, mint a jelenlegi legrosszabb más: break return q
A gyerekek szétválogatásának ötlete nemcsak ideológiailag megkérdőjelezhető, hanem a hatékonysága is. Ha n kicsi, akkor gyorsabb lehet, ha a min-t a megfelelő számú alkalommal megcsinálod, vagy valami hasonló.

Vagyis mi ezeknek a fáknak az általános jelentése: a legközelebbiek keresésekor a pontok távolságát nagyjából az azokat tartalmazó csomópont távolságaként becsüljük meg, a távoliakat eldobjuk, és ennek eredményeként csak a közeli csomópontok pontjai maradnak meg. amelyek nem olyan sokak.

Miért van másra szükség

A kérdés persze az, hogy kik vannak még itt. Nincsenek statisztikám, és nem tudom, mi a fő alkalmazás. Azonban.

3D grafika, egy sugárkövető algoritmus, amely lehetővé teszi fényképes minőségű képek készítését a fényjátékkal, a visszaverődésekkel, a fénytörésekkel és egyéb diffrakciókkal. Nem működik túl gyorsan. Az algoritmus futása közben a fő megoldandó feladat egy adott sugár és a jelenetobjektumok metszéspontjának megtalálása. Ha a tárgyak összetett alakúak (például nem négyzet alakúak), ez nem túl könnyű, és minél összetettebb az objektum alakja, annál nehezebb. A jelenet elég nagy, a tárgy valamiféle felület, háromszögezett (például) és a háromszögek csúcsai határozzák meg. Sok háromszög, valamint csúcs van. A pontok nagyon egyenetlenül oszlanak el a térfogaton, elméletileg a legtöbb sugár elhalad mellette, meg kell érteni, hogy melyek.

Egy KD-fa vagy valami hasonló R-fa felépítése egy objektum köré (amennyire én értem, többé-kevésbé analóg, BVH-nak nevezik), lehetővé teszi, hogy gyorsan megértsük, melyik sugár hová ütközik.

A kép innen származik

Hogyan építsünk

Jaj, ez egy külön probléma, amit nem értettem. Talán egyszer, de most nem. Működik az a KD-fa is, amely ostobán kettéosztja a sejteket (különböző tengelyekre merőlegesen, körben), anélkül, hogy meggondolná, hol lenne jobb síkot rajzolni. Ezzel a megközelítéssel nem ponthalmazból, hanem egyenként hozzáadva építhető fel, ahogy az R-fát leírtam.

Az R-fa felépítésének leírásához csak a csomópont részekre osztásának algoritmusát kell hozzáadni. A homlokban is: két részre osztjuk, kristályosodási központként kiválasztjuk a két legtávolabbi gyereket (a következő szint pontjait vagy csomópontjait, ez O (n ^ 2), ahol n a gyerekek száma a csomópontban), a többit összegyűjtjük a "melyik téglalap tágul kevésbé" elv szerint. Ez az algoritmus másodfokú a csomópontban lévő gyerekek maximális számához képest, az eredmény nem optimális, de úgy tűnik, hogy az optimálishoz kitevő kell. Általában ez is így működik, de ár/minőség arányban akár a legjobb is lehet.

Azt tanácsolom, hogy nézze meg, hogyan oldja meg ezt a problémát a 3D grafikában: KD-tree, BVH. De talán vannak más optimalitási kritériumaik is, itt kell gondolkodnunk. Frissítés: A BVH-ról sajnos nem alkalmazható. Nem csak egy ponthalmaz létezik, hanem ismert az eredeti objektum, amelyből ezt a halmazt kaptuk, és a pontok közötti kapcsolatok. Ezért megengedhetik maguknak, hogy kagylókat építsenek az objektum köré. Ha csak pontok vannak, akkor a téglalapok helyzetének finomításához csak például klaszterezési algoritmusokat alkalmazhat. De nagy valószínűséggel elég sokáig fog tartani.

Ó, igen. A KD fa wiki egészen mást ír le. Azt javasolják, hogy ne tegyenek különbséget a levelek és a belső csomópontok között, hanem minden pontot társítsanak a saját síkjához. Ez egy nagyon őszinte általánosítása egy bináris fának egy többdimenziós térre. Számomra úgy tűnik, hogy ezt nem szabad megtenni. De igazából nem próbáltam ki.

Még egy-két gondolat

Pontosan kettő:

• Nyilvánvaló, hogy az R-fában lévő téglalapokat csak a benne lévő pont találatának számlálási sebessége határozza meg. Vagyis az algoritmusban semmi sem akadályoz meg bennünket abban, hogy bármilyen más alakzatra cseréljük őket. Ha a következtetések levonására való képességem nem változtat, ez lehetővé teszi, hogy a problémát olyan helyzetre általánosítsuk, ahol nincsenek tengelyeink és koordinátáink, hanem csak a halmaz elemei és a köztük lévő távolság érvényes függvénye. Érvényes matematikai értelemben: nem negatív, szimmetrikus, a háromszög szabállyal. Például a vonósok és a már említett Levenshtein távolság. A KD-fa itt nyilvánvalóan nem alkalmazható, mivel itt nincs sík fogalma. És paralelepipedonok sincsenek. És itt vannak a golyók. És úgy tűnik, lehet golyókból fát építeni. Elméletileg elég gyorsan kellene felkínálni az elírási hibák kijavítására vonatkozó lehetőségeket, vajon megcsinálják-e vagy sem? Frissítés: az oda vezető út mentén


• Nem szükséges pontosan pontokat tárolni a fákon. Lehet például golyókat vagy bármilyen más tárgyat. A lényeg, hogy legyen egy függvény a távolság kiszámítására, és hogy a tárgy teljesen beleférjen a cellába, pl. hogy a hozzá való távolság nagyjából a cella távolságaként becsülhető meg. Ez elég lesz a keresési algoritmus megvalósításához.

). k A -d fák a bináris keresőfák egy speciális fajtája.

Matematikai leírás

A k-dimenziós fa egy kiegyensúlyozatlan keresési fa a pontok tárolására $\backslash mathbb(R)^k$. R-fa-szerű keresési képességet kínál egy adott billentyűtartományon belül. A lekérdezés egyszerűsége, memóriaigény rovására $O(kn)$ ahelyett $O((log(n))^(k-1))$.

Vannak homogén és nem homogén k-d fák. A homogén k-d fák esetében minden csomópont tárol egy rekordot. A heterogén változatban a belső csomópontok csak kulcsokat, a levelek rekordokhoz mutató hivatkozásokat tartalmaznak.

Heterogén k-d fában $H\_i(t)\; =\; (x\_1,\; x\_2,\; \backslash lpontok\; ,\; x\_(i-1),\; t\; ,\; x\_(i+1),\; \backslash lpontok,\; x\_k)$ nál nél $1\; \backslash leq\; i\; \backslash leq\; k$ tengellyel párhuzamos $(k-1)$-dimenziós hipersík egy pontban $t$. A gyökér esetében fel kell osztani a pontokat a hipersíkon keresztül $H\_1(t)$ két egyforma nagy ponthalmazba, és írd le $t$ a gyökérre, ettől balra minden olyan pont van tárolva, amelyhez

K-d fa beépíthető $O(n(k+log(n)))$. A tartomány keresése elvégezhető $O(n^(1-\backslash frac(1)(k))+a)$, ahol $a$ a válasz méretét jelöli. A fa memóriaigénye korlátozott $O(kn)$.

Műveletek a k-d fák

Szerkezet

C++-ban leírt fastruktúra:

const int N=10; // kulcsszóközök száma struct Item ( // elemstruktúra int kulcs[N]; // az elemet meghatározó kulcsok tömbje char *info; // eleminformáció ); struct Node ( // fa csomópont szerkezete i. elem; // elem Node *bal; // bal oldali részfa Csomópont *jobb; // jobb részfa )

A fa szerkezete az algoritmus megvalósításának részleteitől függően változhat. Például egy csomópont tartalmazhat egy tömböt, nem pedig egyetlen elemet, ami javítja a keresés hatékonyságát.

Elemkeresés elemzése

Nyilvánvalóan a szkennelt elemek minimális száma $1$, és a megtekintett elemek maximális száma $O(h)$, ahol $h$ a fa magassága. Továbbra is ki kell számítani a megtekintett elemek átlagos számát $A\_n$.

$$ az adott elem.

Fontolja meg az esetet $h=3$. A talált elemek lehetnek:

find(t_1): [(x_0=t_1)]; A=1.

find(t_2): [(x_0

find(t_3): [(x_0>t_1)\land(x_0=t_3)]; A=2.

find(t_4): [(x_0

find(t_5): [(x_0 t_2)\land(x_0=t_5)]; A=3.

find(t_6): [(x_0

find(t_7): [(x_0 t_3)\land(x_0=t_7)]; A=3.

és így tovább az egyes billentyűkhöz. Ebben az esetben az átlagos keresési hossza egy mezőben:

$A=\backslash frac(1+2+2+3+3+3+3)(7)=\backslash frac(17)(7)\backslash kb.\; 2,4$.

Az átlagértéket a következő képlettel számítjuk ki: $A\_n=\backslash összeg\_(k=1)^n\; kp\_(n,k)$

Meg kell találni a valószínűséget $p\_(n,\; k)$. Ő egyenlő $p\_(n,k)=\backslash frac(p\_(A,k))(p\_(n))$, ahol $p\_(A,k)$- hányszor $A=k$és $p\_(n)$ az esetek teljes száma. Ezt nem nehéz kitalálni $p\_(n,k)=\backslash frac(2^(k-1))(2^n-1)$.

Ezt behelyettesítjük az átlagérték képletébe:

A_n=\összeg_(k=1)^n kp_(n,k)=\sum_(k=1)^n (k\frac(2^(k-1))(2^n-1))=\ frac(1)(2^n-1)\sum_(k=1)^n (k2^(k-1))=

\frac(1)(2^n-1)\sum_(k+1=1)^n (((k+1))2^k)=\frac(1)(2^n-1)(\ összeg_(k+1=1)^n (k2^k) + \összeg_(k+1=1)^n (2^k))

\frac(1)(2^n-1)(\sum_(k=1)^n (k2^k) + \sum_(k=1)^n (2^k) - 2^n - n2^n )

=\frac(1)(2^n-1)(n2^(n+2) - (n+1)2^(n+1) +2 - 2^n + 2^3 -1 - n2^n ) = \frac(2^n (n-1) +1)(2^n-1),

azaz $A\_h=\backslash frac(2^h\; (h-1)\; +1)(2^h-1)$, ahol $h$ a fa magassága.

Ha a fa magasságától az elemek számáig megyünk, akkor:

$A\_n=~O(\backslash frac(2^h\; (h-1)\; +1)(2^h-1))\; =\; ~O(h\backslash frac(2^h)(2^h-1)\; -\; 1)\; =\; ~O(log(\backslash frac(n)(N)\; +1)\backslash frac(2^(log(\backslash frac(n)(N)\; +1)))(2^(log(\backslash frac(n)(N)\; )\; +1))-1)\; -\; 1)=~O(log(\backslash frac(n)(N)\; +1)\backslash frac(n+N)(n)-1)\; =$

$=~O(log(\backslash frac(n)(N)\; +1)^(\backslash frac(n+N)(n))-1)$, ahol $N$ a csomópontban lévő elemek száma.

Ebből lehet elkészíteni következtetés hogy minél több elemet tartalmazzon a csomópont, annál gyorsabb lesz a fakeresés, mivel a fa magassága minimális marad, de nem szabad nagy mennyiségű elemet tárolni a csomópontban, mivel ezzel a módszerrel a teljes fa szabályos tömbbé vagy listává fajulhat.

Elemek hozzáadása

Az elemek hozzáadása pontosan ugyanúgy történik, mint egy normál bináris keresőfában, azzal a különbséggel, hogy a fa minden szintjét az a tér is meghatározza, amelyhez tartoznak.

Fa progressziós algoritmusa:

for (int i = 0; fa; i++) // i a térszám if (fa->x[i]< tree->t) // t - medián fa = fa->bal; // mozgás balra részfa else fa = fa->jobbra; // lépés a jobb oldali részfára

A hozzáadás megtörtént $O(h)$, ahol $h$ a fa magassága.

Elemek eltávolítása

A faelemek törlésekor többféle helyzet adódhat:

• A falevél törlése egy meglehetősen egyszerű törlés, ahol egy csomópont törlődik, és az őscsomópont mutatója egyszerűen nullára áll.

• Egy facsomópont (nem egy levél) törlése egy nagyon bonyolult eljárás, melynek során egy adott csomóponthoz a teljes részfát újra kell építeni.

Néha egy csomópont törlésének folyamatát a k-d fa módosításával oldják meg. Például, ha a csomópontunk elemtömböt tartalmaz, akkor a teljes tömb törlésekor a fa csomópontja megmarad, de új elemek már nem kerülnek oda.

Elemek körének megtalálása

A keresés alapja a normál fa leszármazása, ahol minden csomópont egy tartományt ellenőriz. Ha egy csomópont mediánja kisebb vagy nagyobb, mint egy adott térben adott tartomány, akkor a bejárás tovább megy a fa egyik ága mentén. Ha a csomópont mediánja teljesen a megadott tartományon belül van, akkor mindkét részfát meg kell látogatni.

Algoritmus

Z – fa csomópont [(x_0_min, x_1_min, x_2_min,..., x_n_min),(x_0_max, x_1_max, x_2_max,..., x_n_max)] - meghatározott tartomány Funkció Tömb(Node *&Z)( Ha ( bal; // bal oldali részfa ) else If (>Z)( Z=Z->right; // jobb részfa ) Else( // mindkét részfa megtekintése Array(Z->right); // függvény futtatása a jobb oldali részfához Z=Z- >balra; // bal oldali részfa megtekintése ) )

Elemzés

$O(h)$, ahol $h$ a fa magassága. Az is nyilvánvaló, hogy a megtekintett elemek maximális száma $O(2^ó-1)$, vagyis a fa összes elemének megtekintése. Továbbra is ki kell számítani a megtekintett elemek átlagos számát $A\_n$.

$[(x\_(0\_(perc)),\; x\_(1\_(perc)),\; x\_(2\_(perc)),...,\; x\_(n\_(perc))),(x\_(0\_(max)),\; x\_(\; 1\_(max.)),\; x\_(2\_(max.)),...,\; x\_(n\_(max.)))]$- adott tartomány.

A k-d fákról szóló eredeti cikk a következő leírást adja: $A\_n=~O(h\; \backslash cdot\; log(h))$ fix tartományra.

Ha a fa magasságától az elemek számáig megyünk, akkor ez lesz: $A\_n=~O(log(log(n-1))^(log(n-1)))$

A legközelebbi szomszéd megkeresése

A legközelebbi elem keresése két részfeladatra oszlik: a lehetséges legközelebbi elem meghatározása és a legközelebbi elemek megtalálása egy adott tartományban.

Adott egy fa $fa$. A fát megegyezés szerint leereszkedjük a leveleire és a feltétel alapján határozzuk meg a valószínű legközelebbi elemet $l\_(perc)=\backslash sqrt((((x\_0-x[i]\_0))^2\; +\; ((x\_1-x[i]\_1))^2\; +\; ...\; +\; ((x\_n-x[i]\_n\; ))^2))$. Ezt követően a fa gyökeréből elindul egy algoritmus, amely megkeresi a legközelebbi elemet egy adott tartományban, amelyet a sugár határoz meg. $R=l\_(perc)=\backslash sqrt((((x\_0-x[i]\_0))^2\; +\; ((x\_1-x[i]\_1))^2\; +\; ...\; +\; ((x\_n-x[i)\; ]\_n))^2))$.

A keresési sugarat a rendszer módosítja, ha közelebbi elemet talál.

Algoritmus

Z a fa gyökere| Lista - a legközelebbi elemek listája| - a legközelebbi elem keresése Len - a minimális hossz Függvény Maybe_Near(Node *&Z)( // a legközelebbi lehetséges elem keresése While(Z)( // a csomópont elemeinek ellenőrzése for(i=0;i) az aktuális elem hossza)( Len=len_cur; // új hossz beállítása Delete(List); // a lista törlése Add(List); // új elem hozzáadása a listához ) Else if(hosszúságok egyenlőek) Add(Lista); // új elem hozzáadása a listához If((x_0=x[i]_0) && (x_1=x[i]_1) && ... && (x_n=x[i]_n)) Return 1; ) Ha( bal; // bal oldali részfa If(>Z) Z=Z->jobbra; // jobb oldali részfa ) ) Funkció Near(Node *&Z)( // a legközelebbi elem keresése az adott tartományban While(Z)( // a csomópont elemeinek ellenőrzése for(i=0;i) az aktuális elem hossza)( Len=len_cur; // új hossz beállítása Delete(List); // a lista törlése Add(List); // új elem hozzáadása a listához ) Else if(hosszúságok egyenlőek) Add(Lista); // új elem hozzáadása a listához ) If(+len>Z)( // ha a tartomány nagyobb, mint a medián Near(Z->right); // mindkét fa megtekintése Z=Z->balra; ) Ha ( bal; // bal oldali részfa If(>Z) Z=Z->jobbra; // jobb oldali részfa ) )

Elemzés

Nyilvánvaló, hogy a megtekintett elemek minimális száma $O(h)$, ahol h a fa magassága. Az is nyilvánvaló, hogy a megtekintett elemek maximális száma $O(2^ó-1)$, azaz az összes csomópont megtekintése. Továbbra is ki kell számítani a megtekintett elemek átlagos számát.

$[(x\_0,\; x\_1,\; x\_2,...,\; x\_n)]$- egy adott elem, amelyhez a legközelebbi elemet szeretné megtalálni. Ez a feladat két részfeladatra oszlik: a legközelebbi elem megtalálása egy csomópontban és a legközelebbi elem megkeresése egy adott tartományban. Az első részprobléma megoldásához egy leereszkedés szükséges a fán, azaz $O(h)$.

A második részfeladatnál, ahogy azt már kiszámoltuk, az adott tartományba eső elemek keresése ben történik $O(h\; \backslash cdot\; log(h))$. Az átlag meghatározásához egyszerűen adja hozzá ezt a két értéket:

$=~O(h)+\; ~O(h\; \backslash cdot\; log(h))\; =\; ~O(h)\; \backslash cdot\; ((~O(log(h))+1)))$.

Lásd még

Írjon véleményt a "K-dimenziós fa" cikkről

Megjegyzések

Linkek

• , egy nyílt forráskódú STL-szerű megvalósítása k-d fák C++-ban.
• és a fork , hatékony C++ implementációi k-d fa algoritmusok.
• Egy egyszerű C-könyvtár a KD-Trees-szel való munkához
• A hozzávetőleges legközelebbi szomszéd könyvtár tartalmazza a k-d fa megvalósítás
• : véletlenszerűen megvalósított Matlab eszköztár k-d fa a legközelebbi szomszéd gyors, hozzávetőleges kereséséhez, az LSH, a hierarchikus K-Means és az Inverted File keresési algoritmusok mellett.
• , pp. 11 és utána
• pontos és közelítő (k)NN keresési módszerek nyílt forráskódú implementációit tartalmazza k-d fák C++-ban.

Bináris fák Önkiegyensúlyozó bináris fák B-fák előtag fák A tér bináris particionálása Nem bináris fák A tér felosztása Más fák Algoritmusok

Típusok Tömbök Listák fák Számít

Egy K-dimenziós fát jellemző részlet

Natasha elgondolkodott.
– Ó, Sonya, ha úgy ismernéd őt, mint én! Azt mondta... Arról kérdezte, hogyan ígértem Bolkonszkijnak. Örült, hogy rajtam múlik, hogy megtagadjam őt.
Sonya szomorúan felsóhajtott.
– De te nem utasítottad vissza Bolkonszkijt – mondta.
– Lehet, hogy nem! Talán Bolkonskyval mindennek vége. Miért gondolsz olyan rosszat rólam?
„Nem gondolok semmit, csak nem értem…
- Várj, Sonya, mindent meg fogsz érteni. Nézze meg, milyen ember. Ne gondolj rosszat sem rólam, sem róla.
„Senkiről nem gondolok rosszat: mindenkit szeretek és mindenkit sajnálok. De mit csináljak?
Sonya nem adta fel azt a gyengéd hangot, amellyel Natasha megszólította. Minél lágyabb és fürkészőbb volt Natasha arckifejezése, Sonya arca annál komolyabb és szigorúbb volt.
- Natasha - mondta -, megkértél, hogy ne beszéljek veled, én nem, most te magad kezdted. Natasha, nem hiszek neki. Miért ez a titok?
- Újra újra! – szólt közbe Natasha.
- Natasha, félek érted.
- Mitől kell félni?
– Félek, hogy tönkreteszed magad – mondta Sonya határozottan, és maga is megijedt attól, amit mondott.
Natasha arca ismét haragot tükrözött.
„És elpusztítom, elpusztítom, elpusztítom magamat, amint lehet. Semmi közöd hozzá. Nem neked, de nekem rossz lesz. Hagyj, hagyj engem. Utállak.
- Natasha! – kiáltotta Sonya ijedten.
- Utálom, utálom! És te vagy az ellenségem örökre!
Natasha kirohant a szobából.
Natasha többé nem beszélt Sonyával, és elkerülte. Ugyanolyan feldúlt meglepetéssel és bűnösséggel járkált a szobákban, először ezt, majd egy másik elfoglaltságot foglalt el, és azonnal elhagyta őket.
Bármilyen nehéz is volt Sonyának, mindig a barátján tartotta a tekintetét.
Annak a napnak az előestéjén, amelyen a grófnak vissza kellett volna térnie, Sonya észrevette, hogy Natasha egész délelőtt a nappali ablakánál ült, mintha várna valamit, és valami jelet adott az elhaladó katonaembernek. akit Sonya Anatole-nak tévesztett.
Sonya még figyelmesebben kezdte figyelni barátját, és észrevette, hogy Natasha furcsa és természetellenes állapotban van az ebéd és az esti egész ideje alatt (nem megfelelően válaszolt a neki feltett kérdésekre, elkezdte és nem fejezte be a mondatokat, mindenen nevetett).
Tea után Sonya látta, hogy egy félénk szobalány vár rá Natasha ajtajában. Átengedte, és az ajtóban lehallgatva megtudta, hogy a levelet ismét átadták. És hirtelen világossá vált Sonya számára, hogy Natasának valami szörnyű terve van erre az estére. Sonya bekopogott az ajtaján. Natasha nem engedte be.
„El fog menekülni vele! Sonya gondolta. Mindenre képes. Ma valami különösen szánalmas és határozott volt az arcán. Sírva fakadt, elbúcsúzott nagybátyjától – emlékezett vissza Sonya. Igen, így van, rohan vele – de mit tegyek? gondolta Sonya, és most felidézte azokat a jeleket, amelyek egyértelműen bizonyították, miért volt Natasának valami szörnyű szándéka. "Nincs szám. Mit tegyek, írjak Kuraginnak, hogy magyarázatot kérjek tőle? De ki mondja neki, hogy válaszoljon? Írjon Pierre-nek, ahogy Andrej herceg kérte baleset esetén?... De lehet, hogy valójában már megtagadta Bolkonszkijt (tegnap levelet küldött Mary hercegnőnek). Nincsenek bácsik!” Szörnyűnek tűnt Sonyának, hogy elmondja Marya Dmitrievnának, aki annyira hitt Natasában. De így vagy úgy, gondolta Sonya egy sötét folyosón állva: most vagy soha eljött az idő, hogy bebizonyítsam, emlékszem a családjuk jócselekedeteire, és szeretem Nicolast. Nem, nem alszom legalább három éjszakát, de nem hagyom el ezt a folyosót, nem engedem be erőszakkal, és nem hagyom, hogy szégyen a családjukra” – gondolta.

Anatole nemrég költözött Dolokhovba. A Rostova elrablásának tervét Dolokhov már több napig kigondolta és előkészítette, és azon a napon, amikor Sonya, miután Natasát meghallotta az ajtóban, úgy döntött, hogy megvédi őt, ezt a tervet végre kellett hajtani. Natasa megígérte, hogy este tízkor kimegy Kuraginhoz a hátsó verandára. Kuraginnak egy előkészített trojkába kellett volna ülnie, és 60 mérföldre Moszkvától Kamenka faluba kellett volna vinnie, ahol előkészítettek egy csinos papot, akinek feleségül kellett volna vennie őket. Kamenkában készen állt a felállás, aminek a Varshavskaya útra kellett volna vinnie őket, ott pedig postán külföldre vágtattak volna.
Anatole-nak volt útlevele, utazója, és tízezer pénzt vettek el a nővérétől, és tízezret kölcsönzött Dolokhovnak.
Két tanú – Hvostyikov, az egykori hivatalnok, akit Dolohov és Makarin játszott, egy nyugdíjas huszár, egy jó kedélyű és gyenge ember, aki határtalanul szerette Kuragint – az első szobában ült teázni.
Dolokhov faltól mennyezetig perzsa szőnyegekkel, medvebőrökkel és fegyverekkel díszített nagy irodájában Dolokhov utazó beshmetben és csizmában ült egy nyitott iroda előtt, amelyen bankjegyek és pénzköteg hevert. Anatole kigombolt egyenruhájában elsétált abból a szobából, ahol a tanúk ültek, az irodán át a hátsó szobába, ahol a francia lakáj és mások az utolsó holmikat pakolták. Dolokhov megszámolta a pénzt és felírta.
– Nos – mondta –, Khvosztikovnak kétezret kellene adni.
- Nos, engedd meg - mondta Anatole.
- Makarka (így hívták Makarinát), ez érdektelenül neked a tűzön át a vízbe. Nos, vége a pontozásnak – mondta Dolokhov, és egy cetlit mutatott neki. - Így?
„Igen, persze, ez így van” – mondta Anatole, láthatóan nem hallgatva Dolokhovot, és arcáról el nem tűnt mosollyal maga elé nézett.
Dolokhov becsapta az irodát, és gúnyos mosollyal Anatole felé fordult.
- És tudod mit - dobd el az egészet: van még idő! - ő mondta.
- Bolond! – mondta Anatole. - Ne beszélj már hülyeségeket. Ha tudnád... Az ördög tudja, mi az!
– A fenébe – mondta Dolokhov. - Hozzád beszélek. Ez egy vicc, amire készülsz?
- Nos, megint, megint kötekedni? A pokolba került! Huh?... – mondta Anatole összevont szemöldökkel. „A jobboldal nem függ a hülye tréfáidtól. És kiment a szobából.
Dolokhov megvetően és lekezelően mosolygott, amikor Anatole elment.
- Várj egy percet - mondta Anatole után -, nem viccelek, hanem üzleti ügyekről beszélek, gyere, gyere ide.
Anatole ismét belépett a szobába, és megpróbálta összpontosítani a figyelmét, Dolokhovra nézett, nyilvánvalóan önkéntelenül is alárendelve magát neki.
- Figyelj rám, utoljára mondom. Mit viccelődjek veled? keresztbe tettem? Ki intézett el neked mindent, ki találta meg a papot, ki vitte el az útlevelet, ki kapta a pénzt? Mind én.
- Hát, köszönöm. Azt hiszed, nem vagyok hálás neked? Anatole felsóhajtott, és megölelte Dolokhovot.
- Segítettem, de mégis meg kell mondanom az igazat: az ügy veszélyes, és ha szétszeded, hülyeség. Nos, elviszed, oké. Így hagyják? Kiderül, hogy házas vagy. Végül is büntetőbíróság elé állítják...
– Ah! hülyeség, hülyeség! - szólalt meg ismét Anatole grimaszolva. – Mert megmondtam. DE? - És Anatole azzal a különleges előszeretettel (ami a hülye emberekkel bír) arra a következtetésre, hogy saját elméjükkel jut el, megismételte azt az érvelést, amelyet százszor megismételt Dolokhovnak. - Végül is, elmagyaráztam neked, úgy döntöttem: ha ez a házasság érvénytelen - mondta ujját behajlítva -, akkor nem válaszolok; Nos, ha valódi, akkor mindegy: ezt ugye külföldön senki nem fogja tudni? És ne beszélj, ne beszélj, ne beszélj!
- Rendben, gyerünk! Csak magadat kötöd...
– Menj a pokolba – mondta Anatole, és a haját fogva kiment egy másik szobába, azonnal visszatért, és leült egy karosszékre, közel Dolokhovhoz. – Az ördög tudja, mi az! DE? Nézd meg, hogy üt! - Megfogta Dolokhov kezét, és a szívére tette. - Ah! quel pied, mon cher, quel respect! Une deesse!! [O! Micsoda láb, barátom, micsoda tekintet! Istennő!!] Huh?
Dolokhov hidegen mosolyogva, gyönyörű, pimasz szemével ragyogva ránézett, látszólag még szórakozni akart vele.
- Nos, kijön a pénz, akkor mi van?
- Akkor mit? DE? - ismételte Anatole őszinte tanácstalansággal a jövőre gondolva. - Akkor mit? Ott nem tudom, mit… Nos, micsoda hülyeségeket mondjak! Az órájára nézett. - Itt az idő!
Anatole bement a hátsó szobába.
- Nos, hamarosan? Áss ide! – kiáltott rá a szolgálókra.
Dolokhov elvette a pénzt, és egy férfinak kiabálva, hogy rendeljen ételt és italt az útra, belépett a szobába, ahol Hvostyikov és Makarin ült.
Anatole a dolgozószobában feküdt, a karjára támaszkodva, a kanapén, elgondolkodva mosolygott, és halkan suttogott valamit magának gyönyörű szájával.
- Menj egyél valamit. No, igyál egyet! – kiáltotta neki Dolokhov egy másik szobából.
- Nem akarom! - válaszolta Anatole még mindig mosolyogva.
- Menj, Balaga megérkezett.
Anatole felkelt, és bement az ebédlőbe. Balaga egy jól ismert trojka-sofőr volt, aki hat éve ismerte Dolokhovot és Anatolét, és szolgálta őket trojkáival. Nem egyszer, amikor Anatole ezrede Tverben állomásozott, este elvitte Tverből, hajnalban Moszkvába szállította, másnap éjjel pedig elvitte. Nemegyszer vitte el Dolokhovot az üldözéstől, nemegyszer vitette őket a városban cigányokkal és hölgyekkel, ahogy Balaga nevezte. Munkájukkal nem egyszer legyűrte Moszkva környékén az embereket és a taxisokat, és az urai, ahogy ő nevezte őket, mindig megmentették. Egynél több lovat hajtott alájuk. Nem egyszer verték meg, nemegyszer itatták meg pezsgővel és Madeirával, amit szeretett, és mindegyik mögött több dolgot tudott, amit Szibéria egy hétköznapi ember számára rég megérdemelt volna. Kóstoltatásukban gyakran hívták Balagát, kényszerítették, hogy igyon, táncoljon a cigányokkal, és több mint ezer pénzük ment át a kezén. Szolgálatuk során évente hússzor kockára tette életét és bőrét is, munkájuk során pedig több lovat túlterhelt, mint amennyit túlfizettek. De szerette őket, szerette ezt az őrült utazást, óránként tizennyolc mérföldet, szeretett felborítani egy taxit, összezúzni egy gyalogost Moszkvában, és teljes sebességgel repülni a moszkvai utcákon. Szerette hallani maga mögött a részeg hangok vad kiáltását: „Menjünk! elmúlt!" miközben már lehetetlen volt gyorsabban menni; szeretett fájdalmasan felnyúlni a paraszt nyakába, aki egyébként sem halott, sem élő, kerülte őt. – Igazi uraim! azt gondolta.
Anatole és Dolokhov is szerette Balagát a vezetési képességeiért, és amiatt, hogy ugyanazt szerette, mint ők. Balaga felöltöztetett másokkal, huszonöt rubelt vitt el egy kétórás útra, másokkal csak néha ment el, és többnyire a társait küldte. De gazdáival, ahogy ő nevezte őket, mindig maga lovagolt, és soha nem követelt semmit a munkájáért. Csak amikor az inasokon keresztül megtudta, hogy mikor van pénz, néhány havonta egyszer józanul jött reggel, és mélyen meghajolva kérte, hogy segítsen neki. Mindig az urak ültették.

Árfolyamok